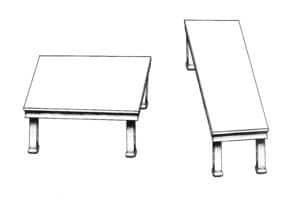
Observez les deux tables ci-dessus. Puis demandez-vous deux choses : quelle est la plus longue et quelle est la plus étroite ? Quelle est la relation entre leur largeur et leur longueur ?
Si vous êtes comme le commun des mortels, vous avez d’abord répondu que la table de gauche est beaucoup plus longue et étroite que celle de droite. Vous avez ensuite répondu que la table de gauche est environ trois fois plus longue que large, alors et celle de droite environ une fois et demie.
Prenez maintenant une règle graduée ou, à défaut, un objet oblong (comme un stylo) et comparez entre elles les longueurs et les largeurs des deux tables. Surprise ! Vous découvrez que les deux tables sont non pas différentes, non pas similaires, mais identiques !! D’ailleurs, vous allez faire l’expérience qu’une seule mesure ne suffit pas. En effet, vous nourrissez secrètement l’espoir que, une fois mesurées les tables, l’illusion s’évanouisse. Or, celle-ci persiste. Vous saisissez donc votre double décimètre et vous mesurez derechef, convaincu que c’est votre mesure et non pas vos yeux qui se trompe. Nenni ! Au sens propre du terme, vous n’en croyez pas vos yeux ! Précisons bien. Même en acquérant la certitude intellectuelle que les deux tables sont identiques, vos yeux continuent à vous dire le contraire, et c’est là un phénomène tout à fait normal et partagé par la quasi-totalité de l’humanité [1]. Il ne s’agit pourtant ni d’un effet sur l’œil (type persistance rétinienne), ni d’une sensation adéquate à son objet (comme lors de la vision d’une cuillère apparaissant brisée par réfraction dans un verre d’eau).
Cette illusion d’optique qui est l’une des « plus puissantes » est connue sous le nom de « tables de Shepard », du nom de son inventeur, le psychologue cognitiviste californien Roger Newland Shepard (1929-2022) [2]. Ce n’est pas le lieu ici d’en analyser la raison. D’un mot, elle tient à ce que, loin d’en rester à la sensation externe, en l’occurrence visuelle, donnant à voir deux parallélogrammes disposés à angle droit, notre cogitative transforme la sensation en perception, c’est-à-dire les voit comme des objets dans un espace tridimensionnel. De plus, l’intelligence interprète aussitôt le dessin comme représentant des tables. Dès lors, d’une part, la dimension la plus longue s’éloignant à l’opposé de nous, nous croyons que ladite « table » de gauche est longue et étroite. D’autre part, interprétant la dimension plus courte comme un raccourci de perspective, nous voyons ladite « table » de droite presque carrée.
Ici, ce qui m’intéresse, c’est l’analogie qu’il est possible de faire entre l’illusion de Sheprd et la blessure de l’intelligence ou du biais cognitif [3]. La similitude porte sur deux points. Le premier est l’erreur : celle-ci ajoute à l’ignorance, l’ignorance de l’ignorance (je ne sais pas que je ne sais pas), c’est-à-dire l’ignorance au second degré (qui scelle la première ignorance : je suis convaincu de mon erreur).
Le deuxième est la profondeur de la blessure qui se traduit par la persistance de l’erreur, même après en avoir été convaincu. C’est ici que joue l’analogie : dans l’illusion sensorielle, même après avoir mesuré et confirmé la mesure, les sens externes continuent à voir la différence entre les deux tables ; dans le biais cognitif, en changeant de régime d’intelligence, en passant de l’intuition (ce que Kahnemann appelle système 1) à l’attention (ce que Kahnemann appelle système 2), l’on peut désintaller la blessure et en guérir. Peut-être serait-il possible, après un long entraînement, de découpler la sensation de la perception et rendre ainsi la prétendue table aux parallélogrammes qui la font voir. Ce travail de désaccoutumance ou de déshabituation serait équivalent à la gymnastique d’un esprit qui, par exemple, cesserait de procéder selon le seul mode mathématique et s’ouvrirait au mode philosophique, voire métaphysique.
Pascal Ide
[1] Les enfants présentant un trouble du spectre de l’autisme sont moins sensibles à l’illusion des tables de Shepard.
[2] Il l’a publiée pour la première fois dans Roger N. Shepard, Mind Sights. Original Visual Illusions, Ambiguities, and Other Anomalies, with a Commentary on the Play of Mind in Perception and Art, New York, Freeman, 1990, p. 128.
[3] Ce rapprochement est inspiré de Richard Thaler et Cass Sunstein, Nudge. La méthode douce pour inspirer la bonne décision, trad. Marie-France Pavillet, Paris, Vuibert, 2010, p. 19-21.