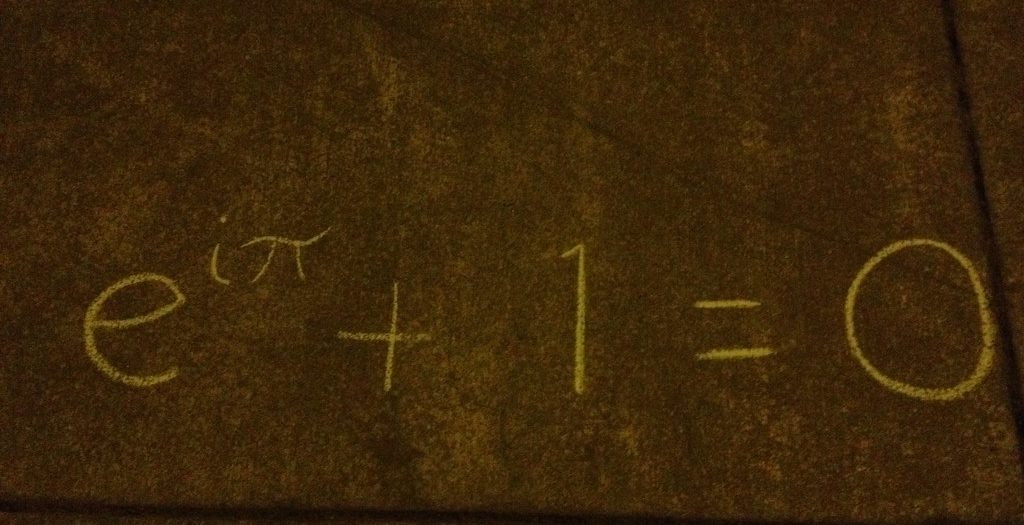« Quand les Pythagoriciens […] découvrirent l’incommensurabilité du rayon et de la circonférence […] cette présence d’un infini réel au sein d’un objet idéalement subsistant et rationnellement défini leur parut si étrange qu’ils placèrent sous la loi du secret cette vérité qui renversait leurs convictions sur l’équation entre le fini et le parfait, entre l’infini et l’inachevé [1] ».
Cette étude fait suite à la précédente : « Le mystère des nombres (1) ».
La métaphysique montre que toute réalité, en ce monde, présente une structure ontophanique (épiphanique ou mystérique), c’est-à-dire se constitue, statiquement, à partir de la bipolarité fond-manifestation et, dynamiquement, à partir du double processus pulsatile de dévoilement et de retrait [2]. Mais cette constitution coextensive à tous les étants naturels vaut-elle aussi pour ces entités si singulières que sont les nombres ? De prime abord, la réponse semble négative : qu’on les considère comme des créations de l’esprit humain (interprétation constructive de la mathématique) ou comme des objets extramentaux (interprétation réaliste de la mathématique), ils semblent parfaitement intelligibles, donc transparents à notre saisie. Sans reste, ils sont donc sans mystère. Nous voudrions défendre la thèse opposée : en son être même, le nombre est mystère. Nous souhaiterions le montrer surtout à partir de l’exemple des nombres transcendants pi (π) et e.
1) Structure ontophanique de π
Prenons l’exemple du nombre π. Le nombre algébrique est une grandeur finiment définissable : il est la solution d’une équation à coefficients entiers. Or, le nombre π n’est pas la solution d’une équation algébrique. En termes concrets : « toute formule faisant intervenir des puissances de π, des entiers, des multiplications, des additions, des soustractions (et des parenthèses), aussi longue soit-elle, ne vaut jamais 0 [3] ». Plus encore, cela vaut même si l’on ajoute « tous les nombres algébriques que l’on veut dans les coefficients des équations ». Par conséquent, le nombre π n’est pas finiment définissable. Autrement dit, « c’est un nombre qui cachait l’infini en lui ». Certes, les nombres naturels, réels sont infinis, mais ils le sont en leur suite qui, elle-même, est dénombrable. Le nombre π, lui, est infini en lui-même, et cette infinité est non-dénombrable, au sens qui vient d’être défini. Cette particularité si singulière a suscité une dénomination propre : elle est qualifiée, en mathématique, de « transcendante ». π est un nombre transcendant (comme e, et une infinité d’auters nombres).
Différents signes le confirment. Par exemple, il est possible de connaître et démontrer de façon rigoureuse beaucoup de propriétés de π sans avoir à le calculer. Détaillons une autre propriété, d’ailleurs paradoxale. 1. Les décimales composant π en base 10 sont aléatoires. Certes, on peut noter quelques singularités ; mais celles-ci sont toujours isolées (quand elles ne sont pas erronées !) ; tôt ou tard, les décimales se présentent comme des chiffres tirés au hasard : elles ne sont pas déductibles, prévisibles, compressibles, etc. Comparativement, π ne présente jamais de suite périodique à partir d’un certain chiffre comme les nombres irrationnels. Par exemple, l’on a remarqué que les « 0 » étaient rares au début de la suite : c’est ainsi que le premier « 0 » n’apparaît qu’à la position 32 ; de même, il n’y a que deux « 0 » dans les 50 premières décimales. Mais on en rencontre 8 dans les 100 premières et 19 dans les 200 et ce nombre s’approche de plus en plus de la moyenne statistiquement attendue. Par conséquent, cette anomalie des débuts se résout vite pour cesser de devenir significative. On pourrait aussi le montrer à partir de la présence de séquences de décimales dignes d’attention : c’est ainsi qu’on trouve une séquence de 6 « 9 » successifs entre les positions 762 et 767 ; de même, dans les deux premiers milliards de décimales, on rencontre une séquence de 10 « 6 » et la séquence « 123456789 ». Mais, interpréter en termes de probabilités, la surgie de ces phénomènes n’a rien de rare. De manière plus générale, Y. Kanada, qui, en 1995, a calculé les 6 442 450 000 premières décimales de π, puis a étudié la fréquence avec laquelle les chiffres approchaient de 1/10, a montré que le résultat « est conforme à ce que l’on obtiendrait par un tirage au hasard équitable [4] ». 2. Or, tout dit combien π n’est en rien un chiffre aléatoire : il « n’est pas un nombre choisi au hasard, c’est un nombre parfaitement déterminé et exceptionnel [5] ». On serait donc tout au contraire en droit d’attendre que π ne contienne pas de série aléatoire. Plus encore, dans certains systèmes de représentation, l’écriture de π n’est en rien aléatoire : par exemple, en base 2 ou 16, l’on a pu élaborer des formles conduisant à des propriétés particulières ; de plus, des formules de série infinie peuvent être interprétées comme un développement régulier de π, ce qui implique une représentation régulière de π. D’ailleurs, plus simplement encore, π modélise la relation très déterminée, donc finie, entre un cercle et son diamètre. La seule explication possible de ce paradoxe est celle du caractère mystérieux de π : autrement dit, celui-ci présente un extérieur fini qui fonde, manifeste (et voile tout à la fois) son infinité intime.
Une autre propriété de π, mais partagée par les autres nombres algébriques transcendants et irrationnels, est un « quasi-paradoxe ». D’un côté, les calculs montre qu’ils sont équirépartis (c’est-à-dire que la répartition des chiffres 0 à 9 composant les décimales est de 1/10, statistiquement) : les calculs par ordinateurs montrent cette répartition équilibrée. De l’autre, il n’y a aucune démonstration de ce fait « et on ne dispose pas de pistes sérieuses pour l’aborder [6] ». Or, les calculs informatiques sont finis, alors que le nombre de décimales est non borné. Ainsi, cette propriété qu’est l’équipartition n’est qu’une conjecture : presque tous les mathématiciens en sont convaincus, et pourtant aucun ne peut en apporter une argumentation concluante ! Ce paradoxe invite l’auteur de l’article à parler de « l’irréalité des nombres réels ». Je préfère y lire, pour ma part, un exemple des épousailles du fini et de l’infini : celui-ci sommeille sous les espèces de celui-là.
Ajoutons des indices historiques. Le mathématicien Georges Cantor a démontré la transcendance de π ; or, presque simultanément, il a démontré l’existence d’une infinité d’infinis (qu’il ordonne : ce qu’il appelle les transfinis). De plus, la preuve qu’il utilise pour démontrer l’infinité des nombres transfinis est une adaptation du procédé de diagonalisation pour démontrer l’existence d’une infinité de nombres transcendants. Enfin, dans les deux cas, les argumentations se font par l’absurde. Autrement dit, il n’existe pas de démonstration positive ; or, une démonstration est finie, bornée, mesurée ; par conséquent, une fois encore, π dit ici son caractère in-fini, sa résistance à être cerné, clôturé.
On pourrait faire appel à d’autres nombres pour ouvrir à l’infini. L’un des plus étranges est le nombre oméga de Chaitin [7]. Il fut inventé par Gregory Chaitin. Il se définit comme la probabilité qu’une machine universelle (comme un ordinateur) à qui l’on fournit un programme au hasard s’arrête. Comme toute probabilité, il s’agit d’un nombre entre 0 et 1. Il s’écrit comme un nombre présentant un nombre infini de décimales équiréparties ; mieux encore, en ne prenant qu’un chiffre sur n (n étant un nombre entier naturel ou même un nombre premier, voire un carré, etc.) et, plus généralement, en extrayant d’oméga une suite de chiffres par tout moyen calculable, on construit un autre nombre équiréparti.
Or, d’un côté, il est mathématiquement définissable : sa définition est claire et explicite. Cela permet d’en déduire des propriétés : par exemple, sa transcendance ou son équipartition ; de même, on peut montrer qu’oméga est normal dans toutes les bases (ce qui est une singularité : aucun nombre explicitement défini ne possède cette caractéristique). De l’autre, il n’est pas complètement calculable ; autrement dit, il n’est explicitement construit. Concrètement, aucun algorithme ne peut en égrener les chiffres un à un. La suite des chiffres le composant se présente comme une série de tirages aléatoires totalement imprévisibles. En effet, son calcul dépend de conjectures mathématiques irrésolues. Par conséquent, seuls certains de ces chiffres sont évaluables ; très vite le calcul bute. Cette dissociation entre définition et calcul ne doit pas étonner. Elle se rencontre aussi pour π dont on a vu que l’on ne peut déduire toutes les décimales. Si bien que l’on a pu dire de ce nombre si étrange « qu’il détient dans ses chiffres la solution concentrée de tous les problèmes mathématiques [8] ».
Voire, on a montré que le nombre oméga de Chaitin n’est pas le seul qui soit « gravement étrange », mais qu’il appartient à une famille infinie dont un encore plus dramatique : le nombre de Solovay, qui est absolument inconnaissable.
Or, de par sa constitution ontophanique, un être est fini en son apparition (sa species), mais infini en son fond. Par conséquent, π est, très proprement, une entité mystérieuse. Ce nombre voile autant qu’il se dévoile, ou pluôt n’apparaît qu’autant qu’il recèle en lui une infinité : voilà pourquoi la suite des chiffres qui le décrit est infinie.
2) Hiérarchie dans la structure ontophanique
La structure mystérique suppose une bipolarité active, dynamique entre une forme finie et un fond infini.
Or, je me demande si l’on ne peut pas distribuer les différents types de nombres réels en fonction de la place croissante de l’infini en leur sein. Distinguons : les entiers naturels, les entiers relatifs, les nombres rationnels, les nombres irrationnels, les nombres transcendants. Peu importe ici le fait que ces ensembles s’incluent ou non.
Les entiers naturels sont infinis par leur suite, donc de manière extérieure, par adjonction d’autres nombres. Il en est de même pour les entiers relatifs, auxquels il suffit d’ajouter un signe négatif. La seule opération est ici la négation (mais sans l’infinité que peut introduire le négatif, par exemple, en morale : le précepte négatif autorise tout le positif, sans le déterminer). Il ajoute aussi le « 0 » qui, lui, présente une certaine infinité intrinsèque.
Les nombres rationnels présentent une infinité interne individuelle. Chaque nombre présente une infinité intrinsèque. En effet, un nombre rationnel est un nombre à décimales (ou à virgule suivie de décimales) obtenu par fraction. On objectera que ces nombres sont de deux sortes selon que ces décimales sont en quantité finie (par exemple 1/2 = 0, 5) ou infinie (par exemple 1/3 = 0, 33333…). Un simple artifice montrera que cette différence peut être négligée : il suffit de dire que le nombre comportant des décimales en quantité finie peut s’écrire comme une suite infinie de décimales égales à 0 (si l’on reprend l’exemple ci-dessus : 0, 50000000000000000…). Quoi qu’il en soit de cette différence, un tel nombre demeure tout de même fini par sa cause (il est obtenu par la fraction de deux entiers, d’ailleurs naturels ou relatifs) et en son résultat (les décimales sont toujours périodiques à partir d’un certain rang : ou immédiatement – 1/11 = 0, 0909090909…. –, ou médiatement, de manière simple, par suite d’un seul chiffre – 1/6 = 0, 166666666… –, parfois de manière complexe, par suite de plusieurs chiffres – 111/34 = 3,263705882352941176370588235294117, où la séquence 6370588235294117 se répète à l’infini). On peut aussi dire d’un nombre rationnel qu’il est infini extrinsèquement en ce qu’il est possible d’en donner une infinité d’équivalents. C’est ainsi que la fraction p/q égale np/nq, n étant un nombre entier naturel. Concrètement : 3/4 = 6/8 = 9/12, etc. Aussi un mathématicien peut-il dire que « chaque nombre rationnel possède une infinité de visages [9] ». Cette caractéristique tient d’ailleurs à une propriété : l’invariabilité des rationnels vis-à-vis des quatre opérations de calcul.
Les nombres irrationnels, quant à eux, sont aussi des nombres à décimales en quantité infinies, mais dénuées de toute périodicité (par exemple, le nombre d’or : 1, 618…), et donc qui ne sont pas le produit de la division d’un entier par un autre, autrement dit qui ne peuvent pas s’écrire comme une fraction à numérateur et dénominateur entiers. Ils sont donc infinis, en ce qu’ils ne sont le résultat d’aucune fraction (si je ne me trompe) et ce que leur configuration n’est en rien réductible à une suite finie de chiffres répétée de manière infinie. Il demeure que, même possédant une infinité de décimales différentes, ils sont toujours le résultat d’une équation algébrique, parfois très simple (par exemple, la racine carrée de 2 : 1, 4142329…).
Enfin, les nombres transcendants sont non-dénombrables. Ils présentent donc une réelle infinité : dans leur configuration, c’est-à-dire dans leur substance, et dans leur cause, c’est-à-dire leur production mathématique (mais non pas géométrique). Peut-être sont-ils les nombres les plus réellement infinis, donc les plus mystérieux. Auquel cas leur caractère aléatoire serait le signe non pas de leur contingence ou de l’arbitraire, mais d’une réalité autrement plus profonde : leur infinité. En effet, cette infinité indéductible ressemble fort à celle des individus ineffables.
3) Le chiffre e
Moins connu du grand public, moins prisé à cause de sa moindre perméabilité à l’intuition, mais pas moins significatif est le chiffre e, base des logarithmes népériens [10].
D’un côté, ce nombre est infini. Il est égal à 2, 718281828458945235… En effet, à l’instar de π, il s’agit d’un nombre transcendant. On doit à Charles Hermite de l’avoir montré, en 1873 : avant la transcendance de π (1880, par Ferdinand von Lindemann, à partir d’une procédure qui n’est pas sans similitude). Les décimales qui le compose sont infinies, non périodiques et surtout indéductibles : elles ne peuvent s’obtenir comme résultat d’un nombre fini d’opérations mathématiques n’impliquant que les nombres entiers et les quatre opérations.
De l’autre côté, il est fini : même si sa configuration est infinie, il est compris entre 2 et 3 ; de plus, en son opérativité, en sa fonction. En effet, il commande l’évolution des systèmes les plus variés : par exemple, la croissance d’un nénuphar doublant de taille chaque jour ; elle est dite exponentielle et c’est l’initiale de cet adjectif qui sert à dénommer le nombre e. Le mathématicien Benoît Rittaud tente de l’exposer de manière intuitive, mais non sans quelques équations [11]. Soit un chauffeur qui se trouve sur une route droite et dégagée. A à 1 km de son point de départ, il décide que ses deux compteurs, de vitesse et de distance, indiquent la même valeur à chaque instant du temps. Ainsi, à 1 km, il doit faire du 1 km/h, à 2 km, 2 km/h, etc. Autrement dit, il se devra d’accélérer progressivement. Comment décrire la position de l’automobile au fur et à mesure où le temps se déroule ? En effet, la fonction exponentielle (associée à toute valeur de t) est la fonction qui décrit le mouvement d’un mobile dont, en chaque instant (et non pas moment), la position est égale à la vitesse.
Tout le problème vient de ce que la vitesse n’est pas une notion mesurable en soi lorsqu’elle est variable. En effet, variable, la vitesse change à chaque instant ; or, pour être mesurée, elle doit être calculée pendant un certain temps où l’on va arbitrairement considérer qu’elle est constante. Ainsi, plus le laps de temps est bref, donc tend vers l’instant, plus précise sera la vitesse. L’équation sera donc elle-même approximative. A ce premier constat, il faut en joindre un second. Il est nécessaire de généraliser. Si le chiffre s’agrandit, ne risque-t-on pas de perdre l’approximation précédente ? En fait, avec une durée de plus en plus petite, mais un nombre n (qui est l’inverse de la durée) qui calcule le nombre d’approximations, de plus en plus grand, il se trouve que le maillage étant plus fin, l’approximation est meilleure. De fait, le calcul montre que l’équation 1 + 1/n tend vers une valeur limite qui se précise de plus en plus au fur et à mesure où n croît. Cette valeur est égale à e.
Je pense que nous ne sommes pas ici en face d’une coïncidence ou d’un simple fait, mais d’une merveille étonnante, qui révèle une structure fine de la réalité que la mathématique révèle : en ce sens, nous sommes proches d’un mystère, au sens ontologique du terme.
4) L’infinité introduite par les opérations
Jusqu’ici, nous avons considéré les entités isolément. Les nombres (et les chiffres) sont corrélés entre eux par des opérations, comme les concepts le sont par des jugements. Précisément : la commutativité, l’associativité, la distributivité – ce qui permet deux opérations : le développement et la factorisation.
Or, ces différentes opérations introduisent des symétries, des souplesses (en l’occurrence une indifférence à l’ordre des nombres pour la commutativité et l’associativité), qui, elles aussi conjuguent fini et infini. Voire permettent de faire circuler activement fond et apparition.
Et comment ne pas penser à « la plus fabuleuse [12] » des équations, celle que découvrir Leonhard Euler au xviiie siècle. Elle joint pas moins de cinq des constantes les plus fondamentales des mathématiques (0, 1, π, e et i) et trois des opérations elles-mêmes les plus fondamentales des mathématiques (addition, multiplication et exponentiation). Enfin, elle les unit dans l’acte d’harmonisation par excellence en mathématique qu’est l’égalisation, celle-ci étant, au point de vue de la quantité, l’équivalent du jugement au point de vue de l’être :
eiπ + 1 = 0
C’est donc à juste titre que l’on estime que la formule d’Euler est belle au-delà de tout, excessivement belle, dans sa simplicité harmonieuse. [13]
5) Conclusion
Nous conclurons d’abord avec une parole du mathématicien et ingénieur flamand Simon Stévin de Bruges (1548-1620). À l’orée des temps modernes, il notait : « Nous concluons doncques qu’il n’y a aucuns nombres absurds, irrationels, irréguliers, inexplicables ou sourds ; mais qu’il y a en eux telle excellence, et concordance, que nous avons matière de méditer nuict et jour en leur admirable perfection [14] ».
Surtout, nous bouclerons avec la précédente étude. Nous y disions que la métaphysique de l’amour-don est possiblement riche d’une relecture du mystère du nombre. Nous venons d’établir que celui-ci, surtout s’il est transcendant, épouse la structure ontophanique fond-apparition. Or, la raison ultime de cette distinction relève de l’autodonation ad intra : le fond se communique dans la manifestation où il se montre, se dit et se donne [15].
Pascal Ide
[1] Maurice Blondel, « La pérennité de la philosophie et le discernement progressif d’une constante et indispensable médiation », Revue de métaphysique et de Morale, 47 (dernier n° de 1940, paru en 1942), p. 349-363, ici p. 351.
[2] Cf. Pascal Ide, Être et mystère. La philosophie de Hans Urs von Balthasar, coll. « Présences » n° 13, Namur, Culture et vérité, 1995, chap. 1.
[3] Jean-Paul Delahaye, Le fascinant nombre pi, coll. « Bibliothèque Pour la science », Paris, Pour la science, diff. Belin, 1997, p. 160.
[4] Ibid., p. 172. Cf. les développements des p. 169-172.
[5] Ibid., p. 173.
[6] Bernard Barsotti, « L’irréalité des nombres réels », Coll., Le mystère des nombres. Hors-série de Sciences et Avenir, avril-mai 2004, réédité Paris, Éd. le Pommier, 2007, p. 183-193, ici p. 186.
[7] Cf. Jean-Paul Delahaye, Randomness, Unpredictability and Absence of Order. Colloque international sur la Philosophie des probabilités, organisé par le cnrs et l’Institut d’histoire des sciences de Paris, 10-12 mai 1990, Dordrecht, Kluwer Academic, 1993, p. 145-167 ; Ming Li et Paul M.B. Vitányi, Introduction to Kolmogorov Complexity and ts Applications, coll. « Texts in Computer Science », Berlin, Springer Verlag, 32008.
[8] Bernard Barsotti, « L’irréalité des nombres réels », p. 190.
[9] Bastien Fernandez, Le monde des nombres, coll. « Quatre à quatre », Paris, Éd. le Pommier, 2000, p. 18.
[10] Cf., par exemple, Benoît Rittaud, Les nombres extraordinaires, coll. « Le collège de la cité », Paris, Éd. le Pommier et la Cité des sciences, 2009, chap. 7 : « Le nombre e, perle de l’analyse ».
[11] Cf. Ibid., p. 152-159.
[12] Ibid., p. 171.
[13] Cf. Paul Nahin, Dr. Euler’s Fabulous Formula, Princeton (Massachusetts), Princeton University Press, 2006.
[14] Cité par Gilles Godefroy, L’aventure des nombres, coll. « Sciences », Paris, Odile Jacob, 1997, p. 197.
[15] Cf. Pascal Ide, « Métaphysique de l’être comme amour. Quelques propositions synthétiques », La métaphysique, numéro coordonné par Emmanuel Tourpe, Recherches philosophiques, 6 (2018), p. 29-56, 1ère partie.